Circles ⇒⇒ Exercise 10.2

Question 1

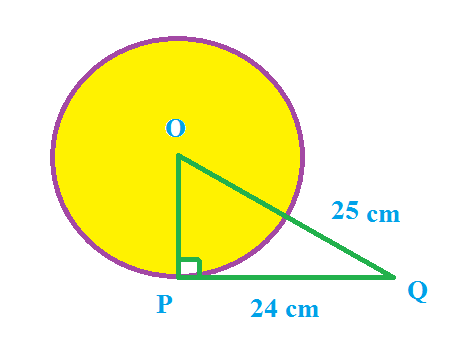
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is:
(A) 7 cm
(B) 12 cm
(C) 15 cm
(D) 24.5 cm

Solution :

Given : PQ = 24 cm. and OQ = 25 cm.

OP is the radius drawn from centre of the circle to tangent.

(Tangent at any point of a circle is perpendicular to the radius throught the point of contact)

∴ OP ⊥ PQ

Since, OPQ is a right triangle, right angled at P.

In Δ OPQ

$ Hypotenuse^2 = Base^2 + Perpendicular^2 $

Using Pythagoras theorem,

$$ OQ^2 = OP^2 + PQ^2 $$

$$ ⇒ (25)^2 = (OP)^2 + (24)^2 $$

$$ ⇒ (OP)^2 = (25)^2 - (24)^2 $$

$$ ⇒ (OP)^2 = 625 - 576 $$

$$ ⇒ (OP)^2 = 49 $$

$$ ⇒ OP = \sqrt {49} $$

$$ ⇒ OP = 7 $$

Therefore option A is correct,OP = 7 cm

Question 2

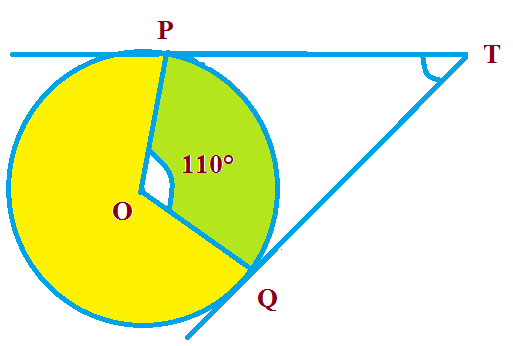
In Figure , if TP and TQ are the two tangents to a circle with center O so that $ \angle $ 110°, then $ \angle $ PTQ is equal to:
(A) 60°
(B) 70°
(C) 80°
(D) 90°

Solution :

Given : $ \angle $ POQ = 110°.

TP and TQ are tangents to the given circle with center O.

Here TP is tangent

∴ OP ⊥ TP

(Tangent at any point of a circle is perpendicular to the radius throught the point of contact)

Hence $ \angle $ OPT = 90°

Now, TQ is also tangent

∴ OQ ⊥ TQ

(Tangent at any point of a circle is perpendicular to the radius throught the point of contact)

Hence $ \angle $ OQT = 90°

Now, TPOQ forms a quadrilateral.

In quadrilateral TPOQ

$$ \angle POQ + \angle OQT + \angle OPT + \angle PTQ = 360° $$

(We know that sum of all interior angles of a quadrilateral = 360°)

$$ 110° + 90° + 90° + \angle PTQ = 360° $$

$$ ⇒ 290° + \angle PTQ = 360° $$

$$ ⇒ \angle PTQ = 360° - 290° $$

$$⇒ \angle PTQ = 70° $$

Therefore option B is correct,$ \angle $ PTQ = 70°

Question 3

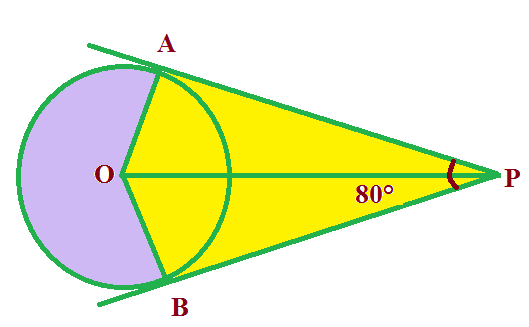
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle 80°, then $ \angle $ POA is equal to:
(A) 50°
(B) 60°
(C) 70°
(D) 80°

Solution :

Given :$ \angle $ APB = 80°

PA and PB are tangents to the given circle with center O.

Here PA is tangent

∴ OA ⊥ PA

(Tangent at any point of a circle is perpendicular to the radius throught the point of contact)

Hence $ \angle $ OAP = 90°

Now, PB is also tangent

∴ OB ⊥ PB

(Tangent at any point of a circle is perpendicular to the radius throught the point of contact)

Hence $ \angle $ OBP = 90°

Now, AOBP forms a quadrilateral.

In quadrilateral AOBP

$$ \angle OAP + \angle APB + \angle PBO + \angle BOA = 360° $$

( We know that sum of all interior angles of a quadrilateral = 360°)

$$ 90° + 80° + 90° + \angle BOA = 360° $$

$$ ⇒ 260° +\angle BOA = 360° $$

$$ ⇒ \angle BOA = 360° - 260° $$

$$ ⇒ \angle BOA = 100° $$

In triangle Δ OAP and Δ OBP

$$ \angle OAP = \angle PBO = 90° $$

$$ OA = OB $$

( OA and OB are radii of same circle )

$$ PA = PB $$

( PA and PB are tangent to same circle from same point P )

( Therefore by SAS Congruence criterion )

$$ {Δ OAP \cong Δ OBP} $$

$$ ∴ \angle AOP = \angle BOP $$

By CPCT

$$ \angle AOP = 100° × {1 \over 2} $$

$$ \angle AOP = 50° $$

Therefore option A is correct,$ \angle $ AOP = 50°

Question 4

Prove that tangents drawn at the ends of a diameter of a circle are parallel.

Solution :

Given

Let AB be a diameter of the circle with center O. Two tangents PQ and RS are drawn at points A and B respectively.

To Prove : PQ || RS

Since PQ is tangent at point A

∴ OA ⊥ PQ

(Tangent at any point of a circle is perpendicular to the radius throught the point of contact)

Hence $$ \angle OAP = 90°.... (1)$$

Now, RS is also tangent at point B

∴ OB ⊥ RS

(Tangent at any point of a circle is perpendicular to the radius throught the point of contact)

Hence $$ \angle OBS = 90° .... (2)$$

From eq. 1 and 2

$$ \angle OAP = \angle OBS = 90° $$

Therefore ,

$$ \angle OAP = \angle OBS $$

i.e. $ \angle $ BAP = $ \angle $ ABS

For lines PQ and RS and transversal AB

Now, $$ \angle BAP = \angle ABS = 90° $$

( Alternate interior angles are equal )

Since the alternate interior angles, $ \angle $ BAP and $ \angle $ ABS, are equal (both are 90° ), the lines PQ and RS must be parallel.
This is a well-known theorem in geometry: if a transversal intersects two lines such that a pair of alternate interior angles are equal, then the two lines are parallel.

∴ PQ || RS

Question 5

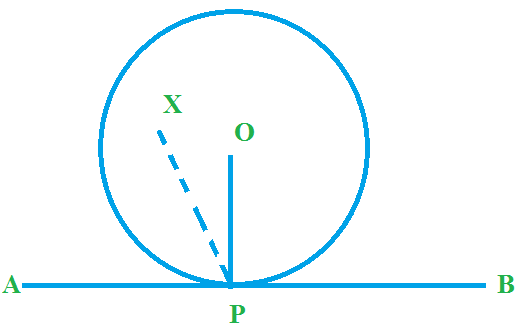
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the center.

Solution :

Given

Let us consider a circle with centre O. Let AB be a tangent which touches the circle at P.

To Prove : Perpendicular to the tangent passes through the center O of the circle.

We shall prove this by contradiction method

we know that the line joining the center and point of contact of a tangent, i.e. radius of the circle is perpendicular to the tangent.

(Tangent at any point of a circle is perpendicular to the radius throught the point of contact)

∴ OP ⊥ AB

Hence $ \angle $ OPB = 90°.... (1)

Let us assume that the perpendicular to AB at P does not pass through centre O. Let it pass through another point X

∴ XP ⊥ AB

Hence $ \angle $ XPB = 90°.... (2)

Comparing eq. 1 and 2

∠ OPB = $ \angle $ XPB = 90°

Therefore , by observation we find

∠ OPB = $ \angle $ XPB is not possible. It is only possible, when the line XP coincides with OP.

Our initial assumption—that the perpendicular line PQ does not pass through the center O—leads to a contradiction. Therefore, the assumption must be false.

Therefore, the perpendicular at the point of contact to the tangent of a circle must pass through the center.

Question 6

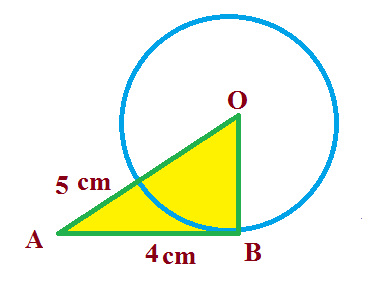
The length of a tangent from a point A at distance 5 cm from the center of the circle is 4 cm. Find the radius of the circle.

Solution :

Let us consider a circle with centre O. Let AB is a tangent drawn on this circle from point A.

Given : OA = 5cm and AB = 4 cm .

OB is the radius drawn from centre of the circle to tangent.

(Tangent at any point of a circle is perpendicular to the radius throught the point of contact)

∴ OB ⊥ AB

Hence $ \angle $ OBA = 90°

So, ABO is a right triangle, right angled at B.

In Δ ABO

$ Hypotenuse^2 = Base^2 + Perpendicular^2 $

( Using Pythagoras theorem, The Pythagorean theorem states that for a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides )

$$ OA^2 = OB^2 + AB^2 $$

$$ ⇒ (5)^2 = (OB)^2 + (4)^2 $$

$$ ⇒ (OB)^2 = (5)^2 - (4)^2 $$

$$ ⇒ (OB)^2 = 25 - 16 $$

$$ ⇒ (OB)^2 = 9 $$

$$ ⇒ OB = \sqrt {9} $$

$$ ⇒ OB = 3 $$

Therefore, the radius of the circle is 3 cm.

Question 7

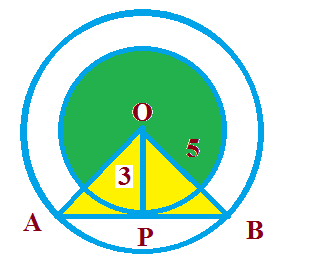
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.

Solution :

Let the two concentric circles be centered at point O.

And let AB be the chord of the larger circle which touches the smaller circle at point P. Therefore, AB is tangent to the smaller circle

To find : Length of AB.

OP is the radius drawn from centre of the circle to tangent.

(Tangent at any point of a circle is perpendicular to the radius throught the point of contact)

∴ OP ⊥ AB

Hence $ \angle $ OPB = 90°

So, OPB is a right triangle, right angled at P.

In Δ OPB

$ Hypotenuse^2 = Base^2 + Perpendicular^2 $

( Using Pythagoras theorem, The Pythagorean theorem states that for a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides )

$$ OB^2 = PB^2 + OP^2 $$

$$ ⇒ (5)^2 = (PB)^2 + (3)^2 $$

$$ ⇒ (PB)^2 = (5)^2 - (3)^2 $$

$$ ⇒ (PB)^2 = 25 - 9 $$

$$ ⇒ (PB)^2 = 16 $$

$$ ⇒ PB = \sqrt {16} $$

$$ ⇒ PB = 4 cm $$

In Δ OPA

$$ Since, OP ⊥ AB $$

$$ PA = PB $$

(Perpendicular from the center of the circle bisects the chord)

$$ AB = 2PA $$

$$= 4 cm × 2 $$

Since P bisects the chord AB, the total length of the chord is twice the length of PA.

$$ AB = 8 cm $$

Therefore, the length of the chord of the larger circle that touches the smaller circle is 8 cm

Question 8

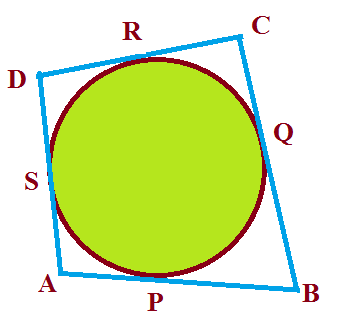
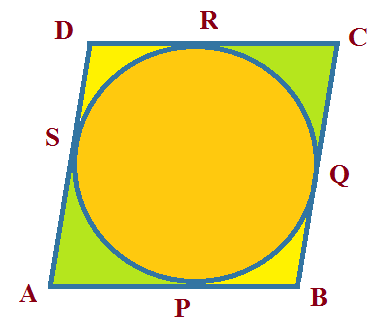
A quadrilateral ABCD is drawn to circumscribe a circle (see figure). Prove that AB + CD = AD + BC

Solution :

Given : A quadrilateral ABCD

To Prove : AB + CD = AD + BC

From the figure we observe that

AP and AS are the tangents to the circle from the same point A .

(Since the length of the tangents drawn from an external point to a circle are equal)

∴ AP = AS ----------- (i)

CR and CQ are the tangents to the circle from the same point C .

(Since the length of the tangents drawn from an external point to a circle are equal)

∴ CR = CQ ----------- (ii)

DR and DS are the tangents to the circle from the same point D .

(Since the length of the tangents drawn from an external point to a circle are equal)

∴ DR = DS ----------- (iii)

BP and BQ are the tangents to the circle from the same point B .

(Since the length of the tangents drawn from an external point to a circle are equal)

∴ BP = BQ ----------- (iv)

Adding all these equations (1,2 and 3,4 ), we obtain.

AP + CR + DR + BP = AS + CQ + DS + BQ

(AP + BP) + (CR + DR) = (AS + BQ ) + (CQ + DS )

(By regrouping)

AB + CD = AD + BC

Hence Proved

Question 9

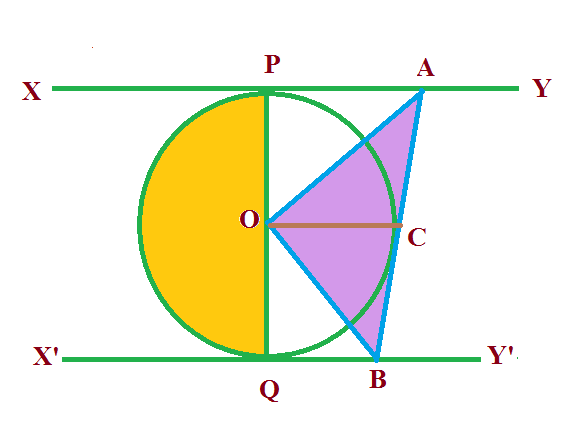
In the given figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that $ \angle $ AOB = 90°

Solution :

Given : A circle with center O

Two tangents XY and X’Y’ are drawn at points P and Q respectively.

And XY || X’Y’

Also , AB is tangent at point C

To Prove :$ \angle $ AOB = 90°

Construction : Let us join point O to C .

∴ OC ⊥ AB

(Tangent at any point of a circle is perpendicular to the radius throught the point of contact)

Hence, $ \angle $ ACO = $ \angle $ BCO = 90°

In triangle Δ OPA and Δ OCA

$$ OP = OC $$

(OP and OC are the radii of same circle)

$$ AP = AC $$

(Since the length of the tangents drawn from an external point to a circle are equal)

$$ OA = OA $$

(Common sides in both of the triangles)

Therefore by SSS Congruence criterion

$$ {Δ OPA \cong Δ OCA} $$

$$ ∴ \angle AOP = \angle AOC ....(i) $$

By CPCT

Similarly ,In triangle Δ OQB and Δ OCB

$$ {Δ OQB \cong Δ OCB} $$

$$ ∴ \angle BOQ = \angle BOC ....(ii) $$

By CPCT

In the given, figure, POQ is the diameter of circle. This means PQ is a straight line.

$$ \angle AOP + \angle AOC + \angle BOC + \angle BOQ = 180° $$

( Linear Pair)

$$ \angle AOC + \angle AOC + \angle BOC + \angle BOC = 180° $$

( From eq 1, $ \angle $ AOP = $ \angle $ AOC and from eq 2,$ \angle $ BOQ = $ \angle $ BOC)

$$ 2 \angle AOC + 2 \angle BOC = 180° $$

$$ 2( \angle AOC + \angle BOC) = 180° $$

$$ \angle AOC + \angle BOC = {180° \over 2} $$

$$ \angle AOC + \angle BOC = 90° $$

$$ \angle AOB = 90° $$

Hence Proved

Question 10

Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.

Solution :

Given : A circle with center O

Two tangents PA and PB are drawn at points A and B respectively.

To Prove :$ \angle $ AOB + $ \angle $ APB = 180°

Construction : Let us join point A to B .

Since PA is tangent at point A

$$ ∴ PA ⊥ OA $$

(Tangent at any point of a circle is perpendicular to the radius throught the point of contact)

Hence $$ \angle OAP = 90°.... (1) $$

Now, PB is also tangent at point B

$$ ∴ PB ⊥ OB $$

(Tangent at any point of a circle is perpendicular to the radius throught the point of contact)

Hence $$ \angle OBP = 90° .... (2)$$

Now, OAPB forms a quadrilateral.

In quadrilateral OAPB

$$ \angle OAP + \angle APB + \angle PBO + \angle AOB = 360° $$

(We know that sum of all interior angles of a quadrilateral = 360°)

$$ 90° + \angle APB + 90° +\angle AOB = 360° $$

(From eq. 1 and 2)

$$ ⇒ 180° + \angle APB + \angle AOB = 360° $$

$$ ⇒ \angle APB + \angle AOB = 360° - 180° $$

$$ ⇒ \angle APB + \angle AOB = 180° $$

Hence Proved

Question 11

Prove that the parallelogram circumscribing a circle is a rhombus.

Solution :

Given : ABCD is a parallelogram which is circumscribing a circle with centre O.

ABCD is a parallelogram

∴ AB = CD and BC = AD ----------- (X)

To Prove : ABCD is a Rhombus . AB = BC = DC = AD

From the figure we observe that

AP and AS are the tangents to the circle from the same point A .

(Since the length of the tangents drawn from an external point to a circle are equal)

$$ ∴ AP = AS ----------- (i) $$

CR and CQ are the tangents to the circle from the same point C .

(Since the length of the tangents drawn from an external point to a circle are equal)

$$ ∴ CR = CQ ----------- (ii) $$

DR and DS are the tangents to the circle from the same point D .

(Since the length of the tangents drawn from an external point to a circle are equal)

$$ ∴ DR = DS ----------- (iii) $$

BP and BQ are the tangents to the circle from the same point B .

(Since the length of the tangents drawn from an external point to a circle are equal)

$$ ∴ BP = BQ ----------- (iv) $$

Adding all these equations (1,2 and 3,4 ), we obtain.

$$ AP + CR + DR + BP = AS + CQ + DS + BQ $$

$$ (AP + BP) + (CR + DR) = (AS + BQ ) + (CQ + DS ) $$

(By regrouping)

$$ AB + CD = AD + BC $$

(From eq. X, AB = CD and BC = AD, )

$$ AB + AB = BC + BC $$

$$ 2AB = 2BC $$

$$ AB = BC ----(Y) $$

Now, from these equations X and Y , we obtain.

$$ AB = BC = CD = AD $$

Hence Proved

Question 12

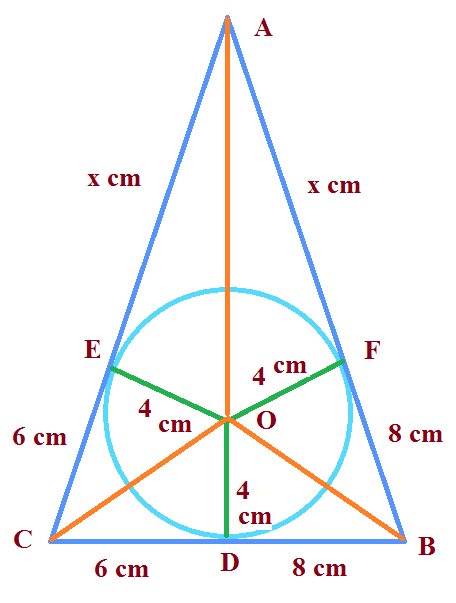
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are lengths 8 cm and 6 cm respectively (see figure). Find the sides AB and AC .

Solution :

Given : A circle with center O, and CD = 6 cm, and BD = 8 cm

Let the circumcircle touches AB and AC at E and F respectively.

Construction : Let us join point OA ,OB , OC and OE , OF .

We have OD = OE = OF = 4 cm.

( radii of same circle)

Also ,

CD = CE = 6cm. and BD = BF = 8 cm. and AE = AF = x cm.

(Since the length of the tangents drawn from an external point to a circle are equal)

Now, we know that, In Δ ABC

$$ 2s = AB + BC + CA $$

$$ 2s = (AF + BF) + (BD + CD) + (AE + CE) $$

$$⇒ 2s = (x + 8) + (8 + 6) + (x + 6) $$

$$⇒ 2s = 2x + 28 $$

$$⇒ s = x + 14 $$

(Where s is the semi-perimeter of triangle)

From above figure

Area of Δ ABC = (Area of Δ OAB + Area of Δ OBC + Area of Δ OCA ) ....(i)

But Area of Δ ABC, according to Heron's Formula, we know that,

Area of Δ ABC = $$ \sqrt {s(s-a)(s-b)(s-c)} $$

$ (s-a) = (x + 14-(x + 8))= 6 $

$ (s-b) = (x + 14-(8 + 6)) = x $

$ (s-c) = (x + 14-(x + 6)) = 8 $

⇒ Area of Δ ABC = $$ \sqrt {(x + 14)(6) (x ) (8) } $$

⇒ Area of Δ ABC = $$ \sqrt {48x(x + 14) } $$

Now, area of Δ OBC = $$ {1 \over 2 } × OD × BC $$

$$⇒ {1 \over 2 } × 4 × 14 $$

$$⇒ 28 $$

And, area of Δ OAB = $$ {1 \over 2 } × OF × AB $$

$$⇒ {1 \over 2 } × 4 × (x + 8) $$

$$⇒ 2 × (x + 8) $$

$$⇒ 2x + 16 $$

And, area of Δ OCA = $$ {1 \over 2 } × OE × CA $$

$$⇒ {1 \over 2 } × 4 × (x + 6)) $$

$$⇒ 2 × (x + 6) $$

$$⇒ 2x + 12 $$

Now putting these values in equation (i)

$$ \sqrt {48x(x + 14)} = 2x + 16 +28 +2x + 12 $$

$$ \sqrt {48x(x + 14)} = 4x + 56 $$

$$ \sqrt {48x(x + 14)} = 4(x + 14) $$

Now by squaring both sides

$$ ⇒ 48x(x + 14) = (4(x + 14))^2 $$

$$ ⇒ 48x(x + 14) = 16(x + 14)^2 $$

$$ ⇒ 48x = {{16(x + 14)^2} \over {(x + 14)}} $$

$$ ⇒ 48x = {16(x + 14) } $$

$$ ⇒ 48x = 16x + 224 $$

$$ ⇒ 48x - 16x = 224 $$

$$⇒ 32x = 224 $$

$$ ⇒ x = 7 $$

Thus, Now, we have AB = x + 8

$$⇒ AB = 7 + 8 = 15 $$

And, AC = 6 + x

$$ ⇒ AC = 6 + 7 = 13 $$

Hence, AB = 15 cm and AC = 13 cm

Question 13

Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle

Solution :

Let ABCD be a quadrilateral circumscribing a circle with O such that it touches the circle at point P, Q, R, S.

P, Q, R, S are the point of contact on sides AB, BC, CD, and DA respectively.

Construction : Let join the vertices of the quadrilateral ABCD to the center of the circle.

Join OP, OQ, OR and OS

To Prove :

$$ \angle AOB + \angle COD = 180° $$

$$ \angle AOD + \angle BOC = 180° $$

Now, In Δ AOP and Δ AOS

$$ OP = OS $$

(OP and OS are the radii of same circle)

$$ AP = AS $$

(Since the length of the tangents drawn from an external point to a circle are equal)

$$ OA = OA $$

(Common sides in both of the triangles)

Therefore by SSS Congruence criterion

$$ {Δ AOP \cong Δ AOS} $$

$$ ∴ \angle AOP = \angle AOS $$

(by CPCT)

$$ \angle 1 = \angle 8 ......(i) $$

Similarily,

$$ \angle 2 = \angle 3 ......(ii) $$

$$ \angle 4 = \angle 5 ......(iii) $$

$$ \angle 6 = \angle 7 ......(iv) $$

In quadrilateral ABCD

$$ \angle 1 + \angle 2 + \angle 3 + \angle 4 + \angle 5 + \angle 6 + \angle 7 + \angle 8 = 360° $$

(We know that sum of all interior angles of a quadrilateral = 360°)

$$ ⇒ (\angle 1 + \angle 8) + (\angle 2 + \angle 3) + (\angle 4 + \angle 5) + (\angle 6 + \angle 7) = 360° $$

(By regrouping)

$$ ⇒ 2 \angle1 + 2 \angle 2 + 2 \angle 5 + 2 \angle 6 = 360° $$

(by eq. 1,2,3 and 4)

$$ ⇒ 2 (\angle1 + \angle 2 + \angle 5 + \angle 6) = 360°$$

$$ ⇒ \angle 1 + \angle 2 + \angle 5 + \angle 6 = 180° $$

$$ ⇒ (\angle 1 + \angle 2 )+ (\angle 5 + \angle 6) = 180° $$

$$ ⇒ \angle AOB + \angle COD = 180° $$

Simiarly, it can be proved that

$$ \angle AOD + \angle BOC = 180° $$

Hence, opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.